本文最后更新于16 天前，其中的信息可能已经过时，如有错误请发送邮件到lieyin2333@163.com <br> 如遇到公式没有加载成功，请刷新几次或耐心等待

RiemannGFM：从结构几何中学习图基础模型

文章发表于WWW 2025 Oral，发布时间 2025.1.29

摘要

基础模型开创了人工智能的新纪元，通过预训练单个模型使其能够在不同数据集上实现跨域迁移。图是无处不在的非欧几里得结构，其应用范围从推荐系统到生化结构。图神经网络在学习图数据方面表现出色，但往往缺乏泛化能力。因此，图基础模型正受到越来越多的关注，受GPT-4显著成功的启发，近期已有不少研究尝试利用大型语言模型。一方面，现有研究主要集中在文本属性图上，而更多的真实图并不包含丰富的文本属性。另一方面，为大型语言模型量身定制的序列图描述忽略了图的一个主要特征——结构复杂性。这些局限性引发了一个重要问题：我们能否超越大型语言模型，预训练一个通用模型来学习任何图的结构知识？在语言或视觉领域，答案是共享词汇表。我们发现，图领域中也存在共享的子结构，这为构建具有结构词汇表（借助该词汇表可构建任何图）的图基础模型带来了新机遇。本文的核心创新在于发现了一种简单而有效的树和环的结构词汇表，并探究了其与黎曼几何的内在联系。在此，我们提出了一种采用几何对比学习的通用预训练模型——RiemannGFM。具体而言，我们首先构建了一种新颖的乘积丛，以整合词汇表的多种几何结构。在这个构建的空间上，我们堆叠黎曼层，使结构词汇表（无论具体图如何）都能在黎曼流形中学习。这为跨域迁移提供了共享的结构知识，并在切丛中为任意输入图生成节点编码。实证结果表明，RiemannGFM在多种真实图上均表现出优越性。

1 Introduction

GFM：图基础模型，不同于为特定任务设计训练的GNN（缺乏泛化能力），GFM（Graph Foundation Model）在广泛的图数据进行预训练，可以适应各种下游图任务的模型。但其研究仍处于婴儿阶段。

基础模型在 AI 领域开启新纪元，但图作为非欧几里得结构（如推荐系统、生化结构），现有图神经网络（GNN）泛化能力弱，需针对特定任务重训练。
现有 GFM 存在两大局限：一是聚焦文本属性图，无法覆盖无丰富文本属性的大量真实图；二是为适配大语言模型（LLM）的序列图描述忽略了图的核心特征 —— 结构复杂性，且多基于欧几里得空间，难以建模复杂结构。

论文尝试超越大语言模型，预训练一个通用模型来学习图的结构知识。通过共享词汇表在语言或视觉领域方面的作用，在图领域中也找到了一个共享的子结构，来构建具有结构词汇表的图基础模型。从简单有效的树（双曲空间）和环（超球面空间）的结构词汇表，探究其与黎曼几何的内在联系，由此提出全新的通用预训练模型RiemannGFM。

论文首次将切丛引入图域，耦合黎曼流形及其周围的切线空间，从流形上的节点坐标嵌入局部几何，同时切线空间中的节点编码容纳了图结构的信息，从黎曼几何的框架中提出了一个通用预训练模型RiemannGFM。RiemannGFM堆叠了通用黎曼层，由词汇学习模块和全局学习模块组成。词汇学习模块将结构词汇嵌入黎曼流形。对于每个子结构，在流形中表述交叉几何注意力，推导出流形保留线性运算。全局学习模块负责更新节点编码。在图中采样多个子结构，首先通过提出的丛卷积进行子结构级聚合，解决切丛不兼容的问题，然后利用几何中点和平行移动计算图级节点编码。最后，在不同几何结构提供的不同视图之间进行几何对比学习，使RiemannGFM能够为任意图生成信息丰富的节点编码。

贡献亮点。

GFM方面，将GFM应用于更广泛的真实图，而不只是文本属性图。（首次从结构几何角度研究GFM）
通用黎曼预训练，提出了新颖的RiemannGFM，为跨域迁移能力提供共享的结构知识。
大量实验，在多种真实图上评估了 RiemannGFM 在跨域迁移学习和少样本学习中的优越性。

2 预备知识

黎曼几何

从几何角度来看，复结构与黎曼流形相关，黎曼流形是赋予黎曼度量 $g$ 的光滑流形 $\mathcal{M}$ 。流形中的每个点 $x$ 都与一个切空间 $\mathcal{T}_x\mathcal{M}$ 相关联，度量 $g$ 即在该切空间上定义。

切空间与流形之间的映射通过指数映射和对数映射实现，同时平行移动负责两个切空间之间的转换。
两点之间的测地线是流形上连接这两点的最短长度曲线。
曲率 $\kappa_x$ 是衡量曲面在点 $x$ ，处偏离平面程度的几何量。当且仅当曲率 $\kappa_x$ 在各处都相等时，流形被称为常曲率空间（CSS）。常曲率空间分为具有负曲率的双曲空间 $\mathcal{H}$ 、具有正曲率的超球面空间 $\mathcal{S}$ 、以及零曲率欧几里得空间 $\mathcal{E}$ 。

洛伦兹/球面模型（Lorentz/Spherical Model）

在这里，论文给出了双曲空间和超球面空间的统一形式，即具有恒定曲率 $\kappa(\kappa\neq 0)$ 的 $d$ 维CCS定义在光滑流形 $\mathcal{L}^d_\kappa=\{x=\left[\begin{matrix}x_t \\ x_s\end{matrix}\right]\in\mathbb{R}^{d+1}|\langle x,x\rangle_\kappa=\frac{1}{\kappa},x_t>0,x_s\in\mathbb{R}^d\}$ 。

即我们将双曲/超球面空间统一表示为 $(d+1)$ 维欧式空间中的一个光滑流形 $\mathcal{L}^d_\kappa$ ，其中

每个点 $x$ 由 $x_t$ （时间维度）和 $x_s$ （空间维度）组成

$\langle x,x\rangle_\kappa$ 表示曲率感知内积，具体如下

$$\langle x,y\rangle_\kappa:=\text{sgn}(\kappa)x_ty_t+x_s^\top y_s,\;\;\;x,y\in\mathcal{L}^d_\kappa\tag{1}$$

其中sgn为符号函数（ $\pm 1$ ）。

基于上述内积可在空间中每个点 $x$ 处诱导出黎曼度量 $g_x$ ，其形式为对角矩阵 $g_x=\text{diag}(\text{sgn}(\kappa),1,\dots,1)$ ，并定义了一个“北极点” $o=\left[\dfrac{1}{\sqrt{|\kappa|}},0,\dots,0\right]^\top$ 。

当 $\kappa<0$ 时， $\mathcal{L}^d_\kappa$ 即为双曲空间的洛伦兹模型（Lorentz Model）， $\kappa>0$ 时为超球面空间的球面模型（Spherical Model）。

符号定义和问题建模

图 $\mathcal{G}$ 由节点集合 $\mathcal{V}$ 和边集合 $\mathcal{E}\subseteq\mathcal{V}\times\mathcal{V}$ ，每个节点可选择性地关联一个属性 $x$ 。类比语言领域的基础模型，GFM旨在预训练一个由参数 $\Theta$ 表征的单一通用模型 $\Phi$ ，可以适配其他图数据，为下游任务生成有效的表征 $z$ 。模型 $\Phi$ 具有跨域迁移能力，即在某一领域预训练得到的参数 $\Theta$ ，在轻微调整后就可以应用于另一领域。文章认为，图基础模型还应具备对任意图的通用性（不仅限于文本属性图），并强调图固有的结构几何特征 —— 这一特征在以往的图基础模型中被大量忽略。

3 RiemannGFM：学习黎曼几何中的结构词汇

RiemannGFM能够学习结构知识，在更广泛的真实图之间提供跨域迁移能力。核心创新点在于，它为任何图结构找到了一种有效的结构词汇，并探究它与黎曼几何之间的关系。

定义1（结构词汇表Structure Vocabulary）:当一组子结构能构建任意图形时，它们被称为结构词汇表。

结构词汇与CCS

对于语言模型，文本会被分解为更小的单位（如单词），通过对这些单位的共性和可迁移性进行编码。在RiemannGFM中，结构词汇表的具体构成被设定为树和环这两类基础子结构。

树结构→双曲空间：利用双曲空间低维有界失真的特性，精准保留树的层级与距离信息，避免欧几里得空间嵌入的失真问题；
环结构→超球面空间：利用超球面空间的旋转不变性，与环的结构特性对齐，确保环的拓扑信息在建模中不丢失。

整体结构

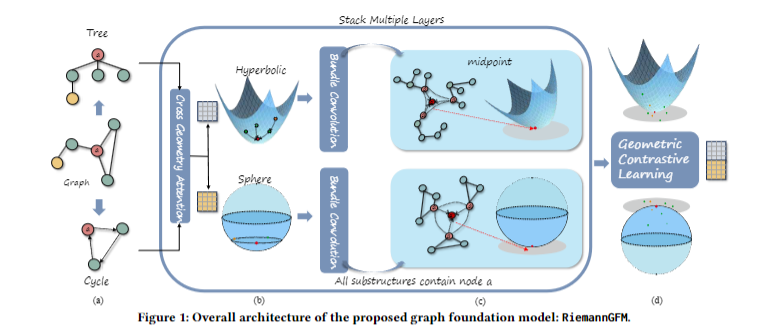
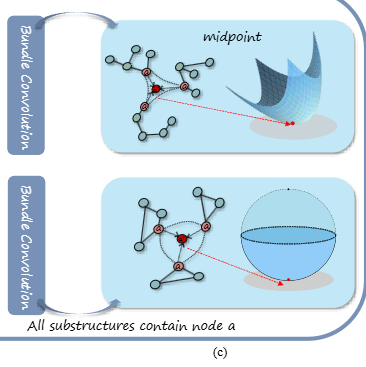
基于词汇中多样的子结构，论文在乘积丛（product bundle）上设计了RiemannGFM。结构如上。根据结构化词汇，首先对图中的树和环进行采样，如(a)。随后，在乘积丛上堆叠通用黎曼层，包括(b)中的词汇学习模块和(c)中的全局学习模块。在不进行图增强的情况下，通过(d)中的几何对比损失进行预训练。

3.1 通用黎曼层 Universal Riemannian Layer

论文将通用黎曼层堆叠再乘积丛上，其中词汇学习模块执行跨几何注意力机制，将结构词汇嵌入到CSS中，使其不受特定图的限制。全局学习模块通过全局视角对齐不同的子结构，并通过提出的丛卷积生成节点编码。

3.1.1 乘积丛上的层

在黎曼几何中，切丛通常由强调局部几何的CCS和描述互补信息的切空间组成。

切丛：一个光滑流形 $\mathcal{M}$ ，其周围附着了互不相交的切空间的并集，数学表达式记为： $\mathcal{TM}=\cup_{x\in\mathcal{M}}\mathcal{T}_x\mathcal{M}$

在这里，切丛的每个节点都与节点坐标和节点编码相关联。流形节点 $p_i\in\mathcal{M}$ 中的坐标包含子结构中的相对位置（即结构词汇），而切空间 $z_i\in\mathcal{T}_{p_i}\mathcal{M}$ 中的编码承载着图层面的全局结构信息。为了整合不同几何结构的子结构，将乘积丛构造为：

$$\mathcal{P}^{d_p}=(\mathcal{H}^{d_H}_{\kappa_H}\otimes\mathcal{T}\mathcal{H}^{d_H}_{\kappa_H})\otimes(\mathcal{S}^{d_S}_{\kappa_S}\otimes\mathcal{T}\mathcal{S}^{d_S}_{\kappa_S}),d_P=2d_H+2d_S,\tag{2}$$

$\mathcal{H}^{d_H}_{\kappa_H}$ 表示曲率为 $\kappa_H$ 、维度为 $d_H$ 的双曲空间， $\mathcal{S}^{d_S}_{\kappa_S}$ 表示曲率为 $\kappa_H$ 、维度为 $d_H$ 的超球面空间，分别对应树和环的子结构流形。
$\otimes$ 表示笛卡尔积。
乘积丛由两个子切丛通过笛卡尔积构成，分别处理树结构和环结构后整合。

对于该乘积中的每个节点，我们有 $x_i=[p_i^H||z_i^H||p_i^S||z_i^S]\in\mathcal{P}^{d_P}$ ，其中 $||$ 表示向量拼接，且 $p_i^H\in\mathcal{H}^{d_H}_{\kappa_H}$ 、 $z_i^H\in\mathcal{T}_{p_i^H}\mathcal{H}^{d_H}_{\kappa_H}$ 、 $p_i^S\in\mathcal{S}^{d_S}_{\kappa_S}$ 、 $z_i^S\in\mathcal{T}_{p^S_i}\mathcal{S}^{d_S}_{\kappa_S}$ 。相应地，乘积丛的黎曼度量为 $g_x^\mathcal{P}=g^{\kappa_H}_x\oplus I_{d_H+1}\oplus g^{\kappa_S}_x\oplus I_{d_H+1}$ ，其中 $I_{d_H+1}$ 为（ $d_H+1$ ）维单位矩阵， $\oplus$ 表示直和。在公式（2）中，双曲丛 $\mathcal{H}^{d_H}_{\kappa_H}\otimes\mathcal{T}\mathcal{H}^{d_H}_{\kappa_H}$ 和超球面丛 $\mathcal{S}^{d_S}_{\kappa_S}\otimes\mathcal{T}\mathcal{S}^{d_S}_{\kappa_S}$ 分别对应树和环,此框架可适用于具有任何曲率的多个丛，为简洁起见，使用双丛乘积。在这篇论文中，采用式（1）定义的 $\mathcal{L}^d_\kappa$ 作为双曲空间和超球面空间的统一格式。

3.1.2 黎曼运算的推导

在设计神经架构之前，论文推导出了一种闭形式的黎曼线性操作，并引入几何中点作为数学准备。在黎曼几何中，操作的输出需要严格保留在流形中，即流形保持（manifold preserving）。本文推导了闭形式的黎曼线性变换、指数映射与对数映射。然而，等距性的缺失以及可能存在的映射误差，促使我们提出一种全黎曼形式化方法。

论文基于矩阵左乘构建线性变换：

$$\forall x=\left[\begin{matrix}x_t\\x_s\end{matrix}\right]\in\mathcal{L}^d_\kappa,f_\mathbf{W}(x)=\left[\begin{matrix}1&0^\top \\ 0&\alpha\mathbf{W}\end{matrix}\right]\left[\begin{matrix}x_t\\x_s\end{matrix}\right],\tag{3}$$

其中缩放因子定义为： $\alpha=\dfrac{\sqrt{\kappa^{-1}-\text{sgn}(\kappa)x_t^2}}{||\mathbf{W}_{x_s}||}$ ， $||\cdot||$ 表示 $L_2$ 范数。

$L_2$ 范数： $||x||_2=\sqrt{\sum\limits^n_{i=1}x_i^2}$

定理1（所述运算的流形保持）：

给定 $x\in\mathcal{L}^{d_1}_\kappa$ 且 $\kappa\neq 0$ ，对于任意矩阵 $\mathbf{W}\in\mathbb{R}^{d_1\times d_1}$ ，运算后的结果 $f_\mathbf{W}(x)\in\mathcal{L}^{d_1}_\kappa$ 仍然保持在原流形中。对于任意矩阵 $\mathbf{W}\in\mathbb{R}^{d_1\times d_2}$ ，则有 $f_\mathbf{W}(x)\in\mathcal{L}^{d_2}_\kappa$

在欧氏空间中，聚合运算通常采用算数平均的方法。对于一个点集及其权重 $\{x_i,v_i\}_{i\in\Omega},x_i\in\mathcal{L}^d_\kappa,v_i\in\mathbb{R}$ ,在，在CCS中的算术平均可如下表示：

$$\text{mid}_\kappa(\{x_i,v_i\}_{i\in\Omega})=\dfrac{1}{\sqrt{|\kappa|}}\sum_{i\in\Omega}\dfrac{v_ix_i}{\left|||\sum_{j\in\Omega}v_jx_j||_\kappa\right|},\kappa\neq 0\tag{4}$$

其中 $||x||_\kappa^2=\langle x,x\rangle_\kappa$ 。通过证明可以发现，所定义的均值即为流形上的几何中点。

定理2：算术平均即几何中点：

式（4）定义的算术平均位于流形上，即 $c=\text{mid}_\kappa(\{x_i,v_i\}_{i\in\Omega})\in\mathcal{L}^d_\kappa$ ，且该算术平均即为几何中点，满足 $c=\arg\min_{c\in\mathcal{L}^d_\kappa}\sum_{i\in\Omega}v_id_\kappa^2(c,x_i)$ ，其中 $d_\kappa^2(c,x_i)$ 表示流形 $\mathcal{L}^d_\kappa$ 上两点 $c$ 与 $x_i$ 之间距离的平方。

3.1.3 结构词汇学习模块

这个模块聚焦于子结构，目标是将结构词汇嵌入到常曲率空间中。即将树（环）结构放置在双曲（超球面）空间中。为此，论文提出了一种跨几何注意力机制（Cross-geometry Attention），用于学习子结构中的节点坐标。我们以双曲因子中的树为例，详细进行公式推导。

在双曲流形中，我们采用自下而上的方法更新树结构。节点坐标通过带注意力权重的聚合操作得到，具体公式如下：

$$v_i=\text{mid}(\{v_j,a_{ij}\}_{(i,j)\in\Omega})\in\mathcal{L}^d_\kappa,v_j\in\mathcal{L}^d_\kappa,\tag{5}$$

$$\alpha_{ij}=\dfrac{\exp(\phi([q_i||k_j]))}{\sum_{(i,t)\in\Omega}\exp(\phi([q_i||k_t]))},\tag{6}$$

其中 $j$ 是 $i$ 的子孙节点，我们扩展符号 $j$ ，使其同时包含节点 $i$ 自身坐标的信息。在跨几何注意力机制中，键、查询和值都通过黎曼线性运算得到。 $k_i=f_V(p_i^H)$ 、 $q_i=f_Q(p_i^S)$ 、 $v_i=f_V(p_i^H)$ 。 $\phi$ 可为返回任意标量的函数。最终，节点坐标 $p_H^i$ 被更新为 $v_i$ 。这里查询值 $q_i$ 来自超球面空间 $\mathcal{S}^d_\kappa$ ，目的是利用另一种几何空间的互补信息（相较于在单一几何空间中执行注意力机制，这种设计的优势已在消融实验中得到验证）。这种聚合操作是单向的，每个节点仅通过子孙节点的坐标来确定自身在流形的位置。

3.1.4 全局学习模块

此模块从图中采样多个子结构，对整个图进行研究，从而从全局视角学习节点编码。分为一下两步。

首先，我们在子结构层面研究节点编码。注意节点编码保存在流形周围的切丛中，但流形上某一点的切空间与另一点的切空间并不兼容。因此现有的信息传递方法（GCN，常曲率GCN）都由于空间不兼容无法使用。论文提出了新的名为切丛卷积的方法。在切丛上进行信息传递。任意曲率下的统一公式推导如下：

$$BC_{p_t}(\{p_i,z_i\}_{i\in\Lambda})=\sum_{i\in\Lambda}\left(\alpha_{it}z_i-\dfrac{\kappa\alpha_{it}\langle z_i,p_t\rangle_\kappa}{1+\kappa\langle p_t,p_t\rangle_\kappa}(p_i+p_t)\right),\tag{7}$$

其中， $\Lambda$ 为子结构的节点集合，注意力权重 $\alpha_{it}$ 通过子结构上的公式（6）得到。通过平行移动，可以连接不同的切空间。

平行移动：
在黎曼几何中，基于Levi-Civita的平行移动 $PT_{x\rightarrow y}$ ，会沿着流形 $\mathcal{M}$ 上两点 $x,y$ 之间的测地线，通过线性等距变换，将切空间 $\mathcal{T}_x\mathcal{M}$ 中的向量 $v$ 映射到另一个切空间 $\mathcal{T}_y\mathcal{M}$ 中。

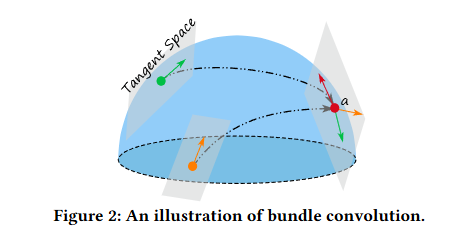
公式（7）可以理解为：首先将各节点的编码平行移动到目标点的切空间，随后在该切空间内进行信息传递。如图2所示，其中 $a$ 为待更新编码的目标点。切丛卷积的优势在于：在封装流形局部几何特征的同时，还能考虑全局结构的编码信息。

第二步，我们在图层面得到输出节点编码。如图1（c）所示，存在3个包含节点 $a$ 的环（树）结构，我们需要对齐节点 $a$ 的坐标并得到图层面的节点编码。对于节点 $a$ 的 $K$ 个采样结果，坐标对其通过流形上坐标的几何中点实现，即 $p_a=\text{mid}_\kappa(\{p_{a_i})_{i=1,\dots,K}\})\in\mathcal{L}^d_\kappa$ ，其中聚合权重设为1。随后将每个采样结果的节点编码平行移动到该中点的切空间中。最终，图层面的节点编码可推导为： $z_a=BC_{p_a}(\{p_{a_i},z_{a_i}\}_{i=1,\dots,K})$ 。

3.2 几何对比学习 Geometric Constrastive Learning

几何对比目标函数如下：

$$\mathcal{J}(H,S)=-\sum^N_{i=1}\log\dfrac{\exp(\langle PT_{p_i^H\rightarrow\boldsymbol{o}}(z_i^H),PT_{p_i^S\rightarrow\boldsymbol{o}}(z_i^S)\rangle)}{\sum^N_{j=1}\exp(\langle PT_{p_i^H\rightarrow\boldsymbol{o}}(z_i^H),PT_{p_j^S\rightarrow\boldsymbol{o}}(z_j^S)\rangle)}\tag{8}$$

整体目标函数定义为： $\mathcal{J}_0=\mathcal{J}(H,S)+\mathcal{J}(S,H)$ ，其中 $N$ 为节点数量。训练流程如算法1，计算复杂度为 $O(|\mathcal{V}|^2+|\mathcal{E}|)$ 。

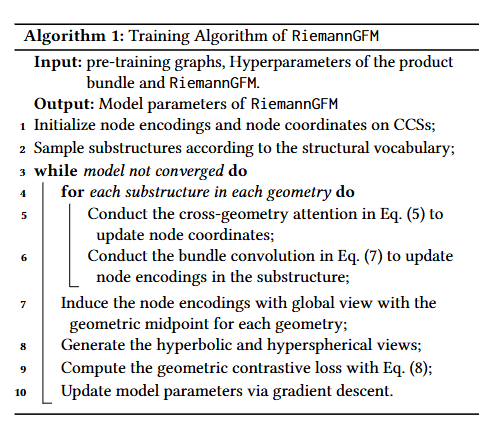
输入：预训练图，乘积丛、RiemannGFM超参数（ $\kappa$ ，子结构采样数，学习率等）
输出：RiemannGFM模型参数。
初始化CCS上的节点编码与节点坐标;
根据结构词汇表子结构采样;
循环至收敛：
for 每个几何空间中的每个采样子结构：
跨几何注意力更新节点坐标，公式（5）；
切丛卷积更新子结构内节点编码，公式（7）；
对每个几何空间，通过几何中点诱导具有全局视角的节点编码；
生成双曲与超球面视图；
通过公式（8）计算几何对比损失；
梯度下降更新参数。

4 实验

本节主要解答如下问题：

RiemannGFM在跨域迁移学习中的表现？
结构词汇表嵌入黎曼几何（而非欧氏几何）的重要性？
少样本学习场景下的表现？
RiemannGFM学到的结构知识的表达能力处于什么水平？
预训练数据集对RiemannGFM的影响？

4.1 实验配置

数据集：含文本属性的图（Citeseer，Pubmed）、含混合属性的图（GitHub，包含用户所在地、标星仓库、雇主及电子邮箱地址）、无属性图（Airports）。

基线：vanilla GNNs（GCN、GraphSAGE）、子监督图学习模型（DGI、GraphMAE2）、图基础模型（OFA、GCOPE、GraphAny、LLaGA、OpenGraph）、RiemannGFM。

评估指标：节点分类：ACC、F1；链路预测：受试者工作特征曲线下面积均值AUC-ROC、AP。独立10次实验取平均值和标准差。

模型配置：输入节点编码由拉普拉斯矩阵给出，其中封装了结构信息。利用了K个最大特征值对应的特征向量，通过预先定义的K对不同的图数据集进行标准化。节点坐标在常曲率空间上通过指数映射进行初始化，以北极点为参考点。对双曲空间和超球面空间采用标准曲率，维度默认设为32。树结构位于双曲空间中，而超球面空间则包含节点三角形和四元组构成的环结构。

4.2 结果评估

RQ1 跨域学习性能

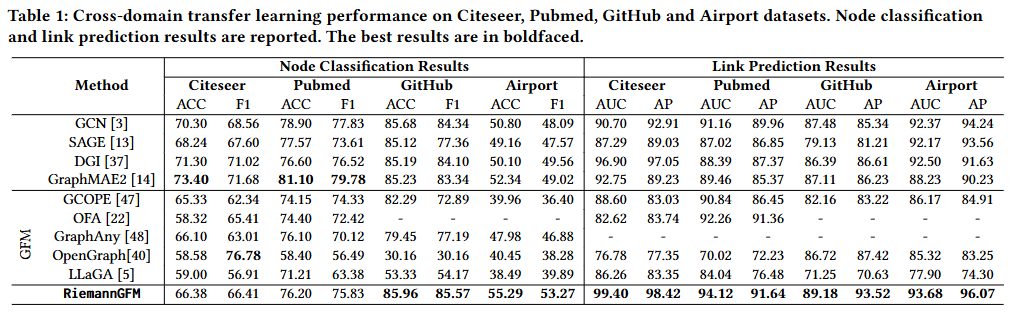
OFA [22] 无法在无文本属性的图上运行。GraphAny仅生成分类逻辑斯蒂输出，因此不能用于链路预测任务。在节点分类任务中，所提出的 RiemannGFM 在无文本属性的图上取得了最佳结果。在含文本属性的图上，RiemannGFM 仍能取得与现有图基础模型相当的性能。这表明构建能够捕捉结构信息的图基础模型具有重要意义。

RQ2 结构词汇表与CCSs的关联

从理论层面来看，双曲空间与树结构具有天然的适配性 —— 这一点可通过 “体积增长一致性” 得到验证；而超球面空间则与环结构存在几何对应关系，其依据是二者共有的 “旋转不变性”。

在实验层面，我们通过 “几何消融实验” 对上述选择进行了实证验证。具体而言，我们将树结构和环结构分别嵌入到双曲空间、超球面空间和欧几里得空间中，并将节点分类与链路预测的实验结果汇总于表2。结果显示：当树结构嵌入双曲空间、环结构嵌入超球面空间时，模型取得了最佳性能 —— 这与我们最初的设计选择完全一致。

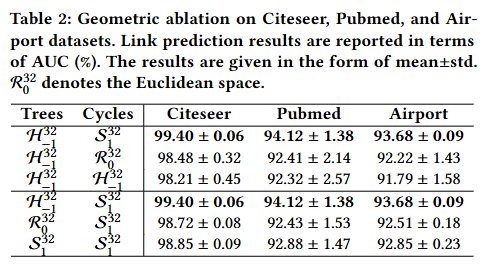
跨几何注意力机制的消融实验

我们引入了一个单几何空间变体模型，该模型在同一常曲率空间内使用键向量、查询向量和值向量。图 3 汇总了不同数据集上的节点分类与链路预测结果。结果显示，跨几何注意力机制（查询向量在对应的另一CCS中）的性能始终优于单几何空间变体模型，这证明了我们设计的有效性。

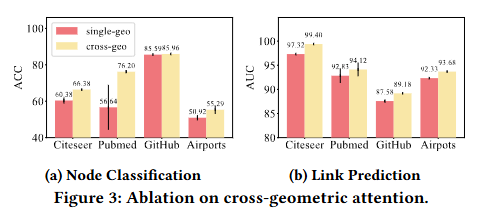
RQ3 少样本学习性能

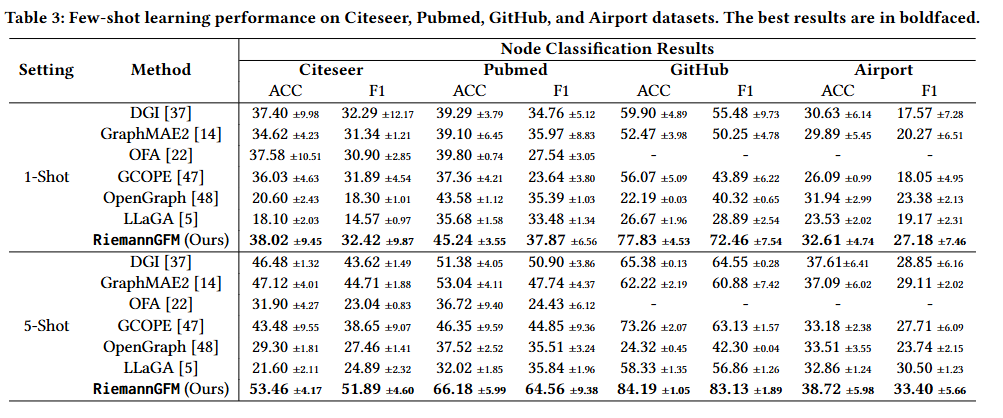
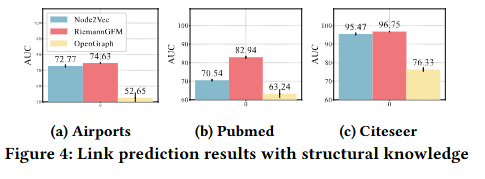
RQ4 结构知识表达能力

论文将 RiemannGFM 的链路预测性能与node2vec以及图基础模型（GFMs）（即OpenGraph）进行了对比分析。在该实验设置中，链路预测任务使用的是预训练完成的 RiemannGFM 生成的节点编码；也就是说，我们仅利用在预训练数据集上学到的结构知识，未引入目标图的属性信息，而 node2vec 则在目标数据集上进行训练。实验结果如图 4 所示。值得注意的是，RiemannGFM 的结构知识不仅能与针对特定图设计的专用模型性能相当，甚至还优于那些融合了属性信息的图基础模型，这充分证明了其出色的表达能力。

RQ5 预训练数据集的影响

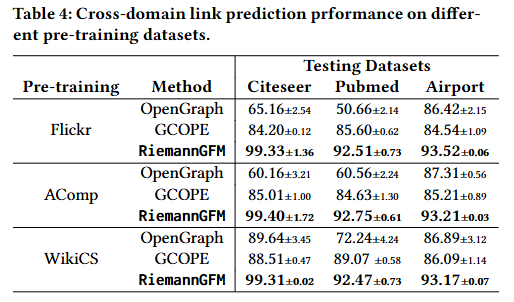
RiemannGFM 在不同预训练图上均表现出更稳定的性能，即预训练数据集对该模型的影响有限。然而，GCOPE 和 OpenGraph 对预训练数据集的要求更高：在相似领域的数据集上进行预训练，能提升下游任务的性能。例如，在 Citeseer 引文网络上进行测试时，OpenGraph 以 WikiCS（引文网络）为预训练数据集时，准确率达到 89.64%；而使用其他领域的预训练数据集时，性能则出现下降（以 Flickr 为预训练数据集时准确率为 65.16%，以 AmazonComputers 为预训练数据集时准确率为 60.16%）。GCOPE 的性能则可能受到不同领域间属性分布差异的影响。

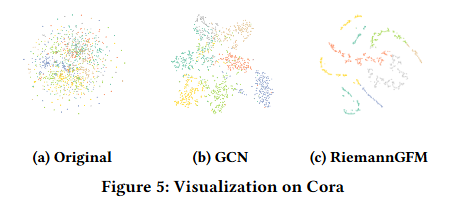
可视化讨论

在此，我们通过 t-sne（t 分布随机邻域嵌入）方法对 Cora 数据集的节点编码进行可视化，结果如图 5 所示，其中不同颜色代表不同的节点类别。结果显示，预训练 RiemannGFM 模型的节点编码相比专用图模型（GCN）的编码具有更好的可分离性，这一现象证明了 RiemannGFM 所学习知识的表达能力。

总结

本研究为构建具有图领域共享结构词汇表的图基础模型（GFM）开辟了新途径。我们的主要贡献在于：发现了与黎曼几何存在内在关联的 “树 - 环” 结构词汇表，并据此提出了通用预训练模型 RiemannGFM。

具体而言，我们首先提出一种新型乘积丛（product bundle），以整合结构词汇表的多种几何特性；在这一构建的空间上，我们堆叠黎曼层（Riemannian layers），使结构词汇表能够脱离特定图的限制，在黎曼流形上完成学习。这一设计为跨域迁移能力提供了共享结构知识，同时通过丛卷积（bundle convolution）为任意图生成含丰富信息的节点编码。大量实验表明，RiemannGFM 在跨域迁移学习和少样本学习任务中均展现出优异性能。