2025.4.22 ACM Web Conference 2025

研究背景

1. 图神经网络（GNN）的局限性
   • 欧氏空间 GNN（如 GCN、GAT）擅长处理网格状、平坦结构数据，但在建模大规模图和捕获层级结构时存在不足。
   • 双曲空间 GNN（如 HGCN、HGAT）借助双曲空间 “指数级距离增长” 特性，能高效表示层级 / 树状结构，却难以处理均匀、平坦的图结构。
   • 现有方法多依赖单一几何空间特性，未充分利用两种空间的互补性，难以高效建模复杂图结构。
2. 对比学习方法的缺陷：传统融合欧氏与双曲 GNN 的对比学习方法，依赖精心筛选正负样本和子图采样，需大量计算资源且调参复杂，限制效率与扩展性。

针对上述问题，本文提出一种名为 Hyperbolic-Euclidean Deep Mutual Learning（H-EDML）的新方法。该方法无需像对比学习方法那样精心选择正负样本，能简洁高效地融合 GNNs 和 HGNNs 的优势，通过深度互学习促进双曲空间和欧几里得空间之间的信息交换与结构交互，实现协同学习。

预备知识

黎曼流形与双曲空间

黎曼流形：$n$维黎曼流形$(\mathcal{M},g)$是一个实光滑流形，并在其每一点$\boldsymbol{x}\in\mathcal{M}$配有内积$g_\boldsymbol{x}:\mathcal{T}_\boldsymbol{x}\mathcal{M}\times\mathcal{T}_\boldsymbol{x}\mathcal{M}\to\mathbb{R}$，其中切空间$\mathcal{T}_\boldsymbol{x}\mathcal{M}$是一个向量空间，可视为流形$\mathcal{M}$在点$\boldsymbol{x}$附近的一阶局部近似。

双曲空间：具有常负曲率的黎曼流形，配备黎曼度量，文中后续所有双曲相关运算均基于其五种等距模型之一 ——庞加莱球模型（Poincaré ball model） 展开。

庞加莱球模型：对于曲率为$-c(c>0)$的$n$为庞加莱球模型，其定义为$\mathbb{D}^n_c=\{x\in\mathbb{R}^n:c||x||<1\}$并具有黎曼度量$g_x^c=\lambda_x^2g^E$，其中$\lambda_x=\dfrac{2}{1-c||x||^2}$是度量缩放因子，$g^E=I_n$为欧几里得度量张量。

双曲空间中的核心运算

莫比乌斯加法：

$$x\oplus_cy:=\dfrac{(1+2c\langle x,y\rangle+c||y||^2)x+(1-c||x||^2)y}{1+2c\langle x,y\rangle+c^2||x||^2||y||^2}\tag{1}$$

其中$x,y\in\mathbb{D}^n_c$，$\langle x,y\rangle$表示欧几里得内积。

莫比乌斯标量乘法：

$$r\otimes_cx:=(\dfrac{1}{\sqrt{c}})\tanh(r\tanh^{-1}(\sqrt{c}||x||))\dfrac{x}{||x||}\tag{2}$$

其中$x\in\mathbb{D}^n_c\setminus\{0\},r\in\mathbb{R}$。

莫比乌斯矩阵-向量乘法：

$$M\otimes_cx:=(\dfrac{1}{\sqrt{c}})\tanh(\dfrac{||Mx||}{||x||}\tanh^{-1}(\sqrt{c}||x||))\dfrac{Mx}{||Mx||}\tag{3}$$

其中$x\in\mathbb{D}^n_c\setminus\{0\},M\in\mathbb{R}^{m\times n}$

指数映射：切空间到双曲空间，

$$\exp^c_x(v)=x\oplus_c(\tanh(\sqrt{c}\frac{\lambda^c_x||v||}{2})\frac{v}{\sqrt{c}||v||})\tag{4}$$

其中$x\in\mathbb{D}^n_c,v\in\mathcal{T}_x\mathbb{D}^n_c\setminus\{0\},\lambda^c_x$为点$x$处的缩放因子。

对数映射：双曲空间到切空间，

$$\log^c_x(y)=\frac{2}{\sqrt{c}\lambda^c_x}\tanh^{-1}(\sqrt{c}||-x\oplus_cy||)\frac{-x\oplus_cy}{||-x\oplus_cy||}\tag{5}$$

其中$x,y\in\mathbb{D}^n_c$且$x\neq y$。

双曲非线性激活函数：

$$\sigma^c(x)=\exp^c_x(\sigma(\log^c_x(x)))\tag{6}$$

其中$x\in\mathbb{D}^n_c$，$\sigma$为欧氏空间中常用的非线性激活函数。

方法实现

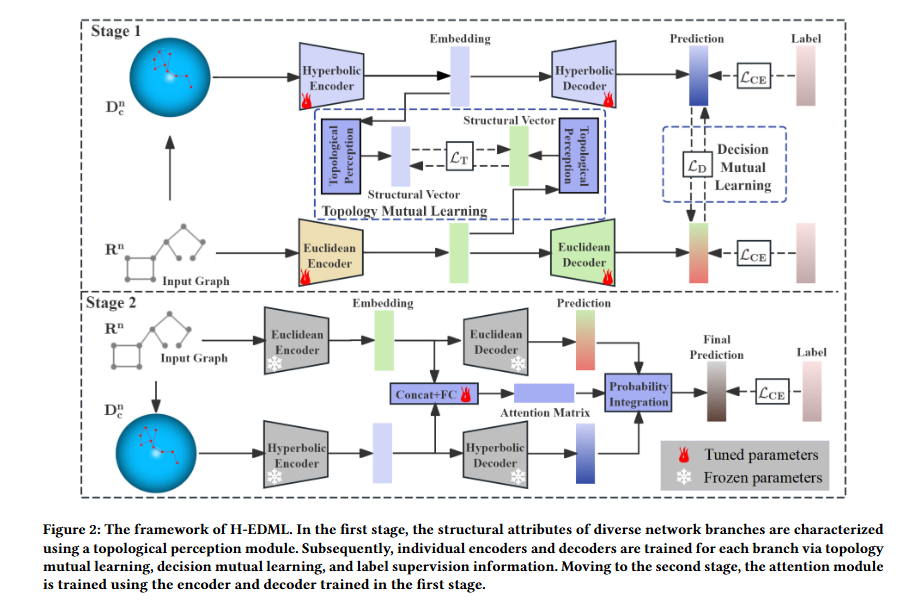
1. 第一阶段：联合训练 GNN 与 HGNN
   此阶段的核心是让 GNN 和 HGNN 通过互学习机制实现信息交互与能力互补。具体而言，会引入拓扑互学习模块（Topology Mutual Learning Module），该模块通过促进两个网络对图整体拓扑结构的感知，增强单一模型对复杂图中不同结构（如层级、扁平）的适配能力；同时，还会集成决策互学习模块（Decision Mutual Learning Module），利用同伴模型输出的软标签（soft label）信息，帮助每个模型修正自身预测偏差，提升决策准确性。此外，两个网络还会同时接受节点标签的监督，确保学习方向与任务目标一致。
2. 第二阶段：训练注意力网络与概率集成
   经过第一阶段训练后，GNN 和 HGNN 已具备各自的优势但可能存在决策差异。为此，第二阶段会固定前一阶段训练完成的 GNN 和 HGNN 参数，利用它们的输出进一步训练一个注意力网络（Attention Network）。该网络通过基于注意力的概率集成策略，为两个模型的预测结果分配动态权重 —— 对当前节点分类更具优势的模型会获得更高权重，最终融合得到更稳健的预测结果，有效缓解不同模型间的决策偏差。

H-E Topology Mutual Learning

输入图为$\mathcal{G}=(\mathcal{V,E})$，节点特征矩阵记为$X\in\mathbb{R}^{N\times d}$，节点$i$特征表示为$x_i$，one-hot标签为$y_i\in\mathbb{R}^M$，$M$为任务中的类别总数。HGNN对节点$i$的嵌入结果与输出概率分布记为$h^H_i,p^H_i$，GNN对应结果为$h^E_i,p^E_i$。

首先通过拓扑感知模块分别提取HGNN与GNN所学习到的图结构属性。对于整个图，提取的结构属性为$\{s_1,s_2,\cdots,s_N\}$，每个节点$i$的结构属性向量为$s_i\in\mathbb{R}^{N_{sample}}$，$N_{sample}$为采样节点数（小型图全节点采样，大型图仅采样中心节点的一阶与二阶邻居）。向量$s_i$中的每个元素$s_{ij}$:

$$s_{ij}=\dfrac{e^{\text{sim}(h_i,h_j)}}{\sum^{N_{sample}}_{j=1}e^{\text{sim}(h_i,h_j)}}\tag{7}$$

其中$\text{sim}(h_i,h_j)$用于衡量节点$i$与节点$j$的嵌入相似度。
由于节点对相似度对应关系并不总是与欧氏距离一致，本文采用核函数刻画节点相似度。

$$\text{sim}(h^E_i,h^E_j)=K(h^E_i,h^E_j)=((h^E_i)^Th^E_j+b)^d\tag{8}$$

$$\text{sim}(h^H_i,h^H_j)=K(h^H_i,h^H_j)=((\log^c_0h^H_i)^T\log^c_0h^H_j+b)^d\tag{9}$$

其中b、c、d固定为0、1、2。

其次通过KL散度衡量差异性，并转化为损失函数。

$$\mathcal{L}^H_T=\sum^{N_{train}}_{i=1}KL(s^H_i||s^E_i)=\sum^{N_{train}}_{i=1}\sum^N_{j=1}s^H_{ij}\frac{s^H_{ij}}{s^E_{ij}}\tag{10}$$

$$\mathcal{L}^E_T=\sum^{N_{train}}_{i=1}KL(s^E_i||s^H_i)=\sum^{N_{train}}_{i=1}\sum^N_{j=1}s^E_{ij}\frac{s^E_{ij}}{s^H_{ij}}\tag{11}$$

其中$N_{train}$为训练集中的节点数量。

H-E Decision Mutual Learning

首先通过KL散度设计决策互学习损失函数。

$$\mathcal{L}^H_D=\sum^{N_{train}}_{i=1}KL(p^H_i||p^E_i)=\sum^{N_{train}}_{i=1}\sum^M_{j=1}p^H_{ij}\frac{p^H_{ij}}{p^E_{ij}}\tag{12}$$

$$\mathcal{L}^E_D=\sum^{N_{train}}_{i=1}KL(p^E_i||p^H_i)=\sum^{N_{train}}_{i=1}\sum^M_{j=1}p^E_{ij}\frac{p^H_{ij}}{p^H_{ij}}\tag{13}$$

同时引入交叉熵损失：

$$\mathcal{L}^H_{CE}=\sum^{N_{train}}_{i=1}H(y_i,p^H_i)=-\sum^{N_{train}}_{i=1}\sum^M_{j=1}y_{ij}\log(p^H_{ij})\tag{14}$$

$$\mathcal{L}^E_{CE}=\sum^{N_{train}}_{i=1}H(y_i,p^E_i)=-\sum^{N_{train}}_{i=1}\sum^M_{j=1}y_{ij}\log(p^E_{ij})\tag{15}$$

最后得到总损失：

$$\mathcal{L}^H=\mathcal{L}^H_{CE}+\alpha_1\mathcal{L}^H_D+\beta_1\mathcal{L}^H_T\tag{16}$$

$$\mathcal{L}^E=\mathcal{L}^E_{CE}+\alpha_2\mathcal{L}^E_D+\beta_2\mathcal{L}^E_T\tag{17}$$

H-E Attention-based Probabilistic Integration

注意力矩阵：

$$A_i=S(\sigma((\delta([\log^c_0(h^H_i),h^E_i]W_1))W_2))\tag{18}$$

其中$[\cdot,\cdot]$表示向量拼接操作，将HGNN与GNN节点拼接后的特征向量输入两层全连接网络（权重分别为$W_1,W_2$），第一层全连接后采用ReLU激活函数（记为$\delta$），第二层全连接后采用Sigmoid函数（记为$\sigma$）。再使用Softmax函数（记为$S$）归一化。

得到的矩阵包含两个元素：

• $A_{i1}$表示分配给HGNN预测分布$p^H_i$的注意力权重，
• $A_{i2}$表示分配给GNN预测分布$p^E_i$的注意力权重。

通过加权求和得到最终概率：

$$p_i=A_{i1}p^H_i+A_{i2}p^E_i\tag{19}$$

实验

实验设置

数据集：

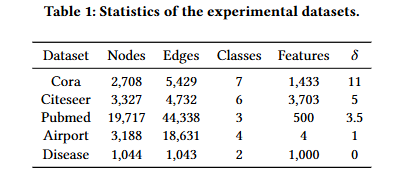
$\delta$表示双曲性，量化数据集的树状结构程度，$\delta$值越低，数据集的梳状特征越显著。

基线：神经网络（NN）：MLP，HNN；欧几里得图神经网络：GCN、GraphSAGE、GAT、SGC、GraphCON、NodeFormer、SGFormer、ACMP；双曲图神经网络：HGNN、HGCN、GIL、HGAT、LGCN、HGCL、F-HNN、H-GRAM、LRN。

实现细节：

• 引文网络（Cora、Citeseer、Pubmed）：采用 GCN [25] 的标准划分方式；
• Airport 数据集：采用 70%（训练）、15%（验证）、15%（测试）的划分比例；
• Disease 数据集：采用 30%（训练）、10%（验证）、60%（测试）的划分比例（因数据集为树状结构，测试集比例更高以验证泛化性）。
• 一致性设置：所有方法使用相同的随机种子初始化，采用相同的早停（early stopping）策略 —— 验证集性能连续 200 个 epoch 无提升则停止训练；
• 参数搜索空间：通过网格搜索（grid search）优化超参数，搜索范围包括：
  • 学习率（Learning rate）：[0.001, 0.005, 0.01, 0.02]；
  • dropout 率（Dropout rate）：[0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6]；
  • 权重衰减（Weight decay）：[0, 1e-4, 5e-4, 1e-3]；
  • 隐藏层层数（Number of hidden layers）：[1, 2, 3]；
• 结果稳定性：所有方法均独立运行 10 次（随机参数初始化不同），最终结果以 “均值 ± 标准差” 形式报告，确保统计显著性。
• 潜在表示维度：所有方法的 latent representation 维度统一设为 16，消除维度差异对性能的影响；
• 双曲 GNN 曲率：所有双曲基线方法与 H-EDML 中的 HGNN 组件，其双曲空间曲率均设为 1；
• H-EDML 基础模型：固定选择 HGAT 作为双曲基础模型，GCN 作为欧几里得基础模型；优化器与硬件：采用 Adam 优化器 [24] 进行参数更新，所有实验在 NVIDIA GeForce RTX 3090 GPU 上完成，基于 PyTorch 框架实现。

实验结果

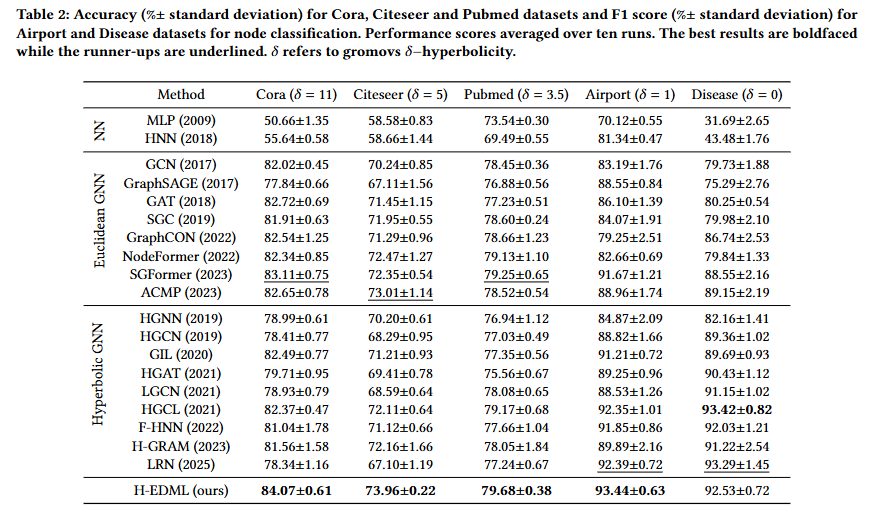
除 Disease 数据集外，H-EDML 在 Cora、Citeseer、Pubmed、Airport 4 个数据集上均取得最佳结果，相较于次优方法的性能提升最高达 1.05%。在Disease数据集中也仅低于转为高双曲性设计的HGCL和LRN。

我们也可以在此表中观察到两个GNN在不同类型数据集中的优势。

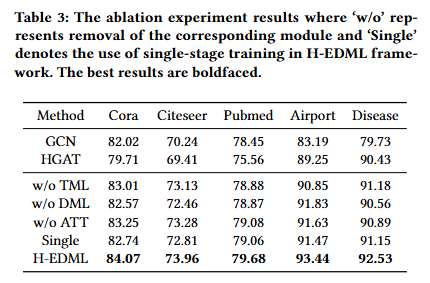
消融实验

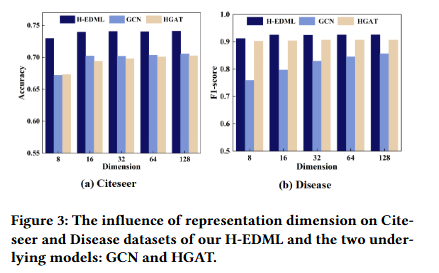
嵌入维度的影响

该实验通过在 “高层级结构数据集（Disease，δ=0）” 与 “弱层级结构数据集（Citeseer，δ=5）” 上设置不同嵌入维度（如 8、16、32、64、128）

不同基础模型的影响

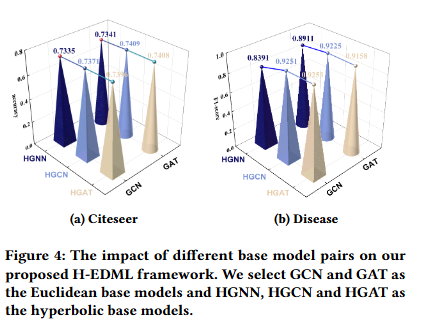
除“HGNN+任意欧几里得模型”的组合外，其他所有基础模型组合（如 GCN+HGAT、GAT+HGCN、GAT+HGAT）在 5 个数据集上均表现优异，且性能差异小于1%。