论文原地址为：GraphMoRE: Mitigating Topological Heterogeneity via Mixture of Riemannian Experts | Proceedings of the AAAI Conference on Artificial Intelligence

发表于：2025-4-11 AAAI

GraphMoRE: Mitigating Topological Heterogeneity via Mixture of Riemannian Experts

GraphMoRE：通过黎曼专家缓解拓扑异质性

什么是拓扑异质性？

拓扑异质性（Topological Heterogeneity）核心指系统的拓扑结构并非均匀一致，而是存在显著差异或局部变化。

拓扑（Topology）：不关注元素的具体位置、距离或大小，只关注元素之间的连接关系（边）。例如：社交网络中 “谁与谁是好友”、材料中 “原子如何键合”、大脑中 “神经元如何连接” 均属于拓扑范畴。

异质性（Heterogeneity）：系统内元素或结构的“非均匀性”和“差异性”，与同质性（Homogeneity）相对。

因此，“拓扑异质性” 本质是：系统的连接模式存在 “局部差异”—— 某些区域的连接密集、结构复杂，而另一些区域连接稀疏、结构简单，或不同区域的连接规则截然不同。

1. 理想图的均质性

• 规则图（Regular Graph）：所有节点的度完全相等（如环图中每个节点度为 2，完全图中每个节点度为 N-1），度分布是 “单点分布”，无任何异质性。
• 随机图（Random Graph）：节点间连接概率均等，度分布近似服从泊松分布，大部分节点的度集中在均值附近，极端度（极高或极低）的节点几乎不存在，拓扑均一性强。

2. 异质图的非均质性

真实异质图的度分布通常服从幂律分布（Power-Law Distribution），表现为 “少数节点拥有极高的度，多数节点度很低”，即存在所谓的 “枢纽节点（Hubs）”。

示例：

• 社交网络中，少数 “网红”“名人”（枢纽节点）拥有数百万粉丝（高 degree），而绝大多数普通用户仅关注几十人（低 degree）；
• 万维网中，谷歌、百度等核心网站（枢纽节点）链接数百万网页，而普通个人博客仅链接少数页面。

这种 “枢纽节点主导连接” 的模式，是图中拓扑异质性最经典的体现。

拓扑异质性对GNN的影响

多数方法（如 GCN、HGCN）在单一常曲率空间中学习图表示，无法匹配复杂几何结构，导致嵌入失真高、质量低。

图神经网络（GNN）的核心机制是通过消息传递（Message Passing）聚合邻居信息来学习节点 / 图表示，其性能高度依赖于对图拓扑结构的建模能力。

• 低 degree 节点：信息匮乏，表示片面
  边缘节点（如社交网络中的普通用户）仅有少数邻居，消息传递时可聚合的信息极少，其表示容易陷入 “欠拟合”—— 无法捕捉足够的拓扑上下文，导致下游任务（如节点分类）中这类节点的预测精度极低。
• 高 degree 枢纽节点：信息过载，表示泛化性差
  枢纽节点（如网红、核心路由器）连接数百 / 数千个邻居，直接聚合所有邻居信息会导致：
  1. 噪声污染：邻居来源复杂（可能跨多个社群），混合聚合会引入大量无关噪声，稀释枢纽节点自身的核心特征；
  2. 计算冗余：处理海量邻居会显著增加模型的计算开销（时间 / 空间复杂度）；
  3. 过度平滑前兆：过多邻居的信息混合易导致枢纽节点的表示 “趋同”，失去对其所属局部社群的针对性。

示例：在学术合作网络中，GCN 对 “高产学者”（高 degree）的表示可能混合了不同领域合作者的信息，反而无法准确反映其研究方向；对 “新人学者”（低 degree）的表示则因邻居少而无法区分其与其他新人的差异。

论文指出：近期的研究表明，乘积流形（product manifold）有望解决这种问题，但其依然是同质的，不足以灵活地表示混合的异质拓扑。本文则提出了新颖的 Graph Mixture of Riemannian Experts(GraphMoRE)框架，通过个性化的细粒度拓扑几何模式保留来有效处理拓扑异质性。

• 从局部拓扑特征描述的角度分析拓扑异质性，为节点构建个性化嵌入空间，以最大限度地减少异构拓扑的失真。
• 首次将 MoE 引入黎曼表示学习，为基于黎曼几何的图基础模型设计提供了新视角。
• 大量实验表明，该方法优于先进的相关方法，凸显了 GraphMoRE 在拓扑异质性方面的潜力。

3 预备知识

1 黎曼流形

光滑流形（Smooth Manifold）

局部平坦，整体可能弯曲

对于空间中的任意一点，都存在一个局部邻域，可以通过一个连续可逆的光滑（无限次可微）映射与$\mathbb{R}^n$中某个开集对应。

例：地球表面（2维球面）是一个2维光滑流形 —— 我们用 “地图集”（多个坐标卡，如中国地图、欧洲地图）覆盖球面，每张地图都是球面局部到平面（$\mathbb{R}^2$）的光滑映射，且相邻地图的重叠区域可以平滑转换。

黎曼度量（Riemannian Metric）和黎曼流形（Riemannian Manifold）

在流形的每一点处定义一个局部的内积运算

对于$n$维黎曼流形$\mathcal{M}$上的任意一点$p$，其切空间（流形在$p$点的“局部切线/切平面”构成的$n$维线性空间，记为$\mathcal{T}_p \mathcal{M}$）上的黎曼度量$g_p$满足：

• 对称性：$g_p(v,w)=g_p(w,v)$（内积的对称性）；
• 正定性：$g_p(v,v)\geqslant 0$，且等号仅当 $v=0$（零向量）时成立（保证长度非负）；
• 光滑性：当$p$在流形上光滑移动时，$g_p$也随之光滑变化。

在$d$维黎曼流形$\mathcal{M}^d$上一点$x$的切空间$\mathcal{T}_x\mathcal{M}^d$中，黎曼度量$g_x$定义了一个正定内积$\mathcal{T}_x\mathcal{M}^d\times \mathcal{T}_x\mathcal{M}^d\rightarrow\mathbb{R}$,用于定义黎曼流形的几何性质和运算。向量$v$在流行$\mathcal{M}^d$和切空间$\mathcal{T}_x\mathcal{M}^d$之间的转换，是通过点$x$处的对数映射$\log_x(v):\mathcal{M}^d\rightarrow \mathcal{T}_x\mathcal{M}^d$和指数映射$\exp_x(v):\mathcal{T}_x\mathcal{M}^d\rightarrow \mathcal{M}^d$来实现的。

在黎曼空间中，图神经网络通常通过$\log_0(\cdot)$将节点映射到切平面进行消息传递和聚合，然后通过$\exp_0(\cdot)$将节点映射回黎曼空间，其中$0$是参考点。

常曲率空间（Constant Curvature Spaces）

曲率是描述空间弯曲程度的几何量。在黎曼流行中，定义了每一点$x$处的截面曲率$\kappa(x)$。对于在所有点处都具有相等截面曲率的流形，将其定义为常曲率空间$\mathcal{M}_\kappa^d$,根据曲率$\kappa$的符号，常曲率空间可分为三类：球面空间（$\kappa>0$）、双曲空间（$\kappa<0$）和欧几里得空间（$\kappa=0$）。它们分别适用于对具有不同拓扑结构的数据进行建模。

2 问题表述

符号说明

图可以表示为$G=(A, X)$，其中$A\in 0, 1^{N\times N}$是邻接矩阵，$X\in\mathbb{R}^{N\times d}$是节点特征矩阵，$N$表示节点数量，$d$表示节点特征的维度。同时分别令$\mathcal{V,E}$作为图的节点集合和边集合。

问题定义

论文主要考虑具有拓扑异质性的图上的黎曼表示学习问题。对于给定的一个图$G=(A, X)$，包含了不同的拓扑模式。论文的目标则是学习一个编码函数$\psi:\mathcal{V}\rightarrow\mathcal{P}$,使这个函数能捕获节点$v$周围的几何特征，并将节点$v$自适应地映射到个性化嵌入空间$\mathcal{P}$中，其中$\mathcal{P}$由不同的曲率空间组成。与现有的混合曲率研究不同，这里将不同的拓扑模式嵌入到相应的最优曲率空间中，以最大限度地保留图结构，而不是将所有节点嵌入到同一个曲率空间中。

4 GraphMoRE

这是一个黎曼专家图混合框架，核心见解为，从局部拓扑特征描述地角度对拓扑异质性进行分解。

首先引入多样化黎曼专家为灵活构建多样化的嵌入空间奠定基础。然后，我们设计了一种拓扑感知门控机制来捕捉节点周围的几何特性，并为每个节点构建个性化的混合曲率空间。

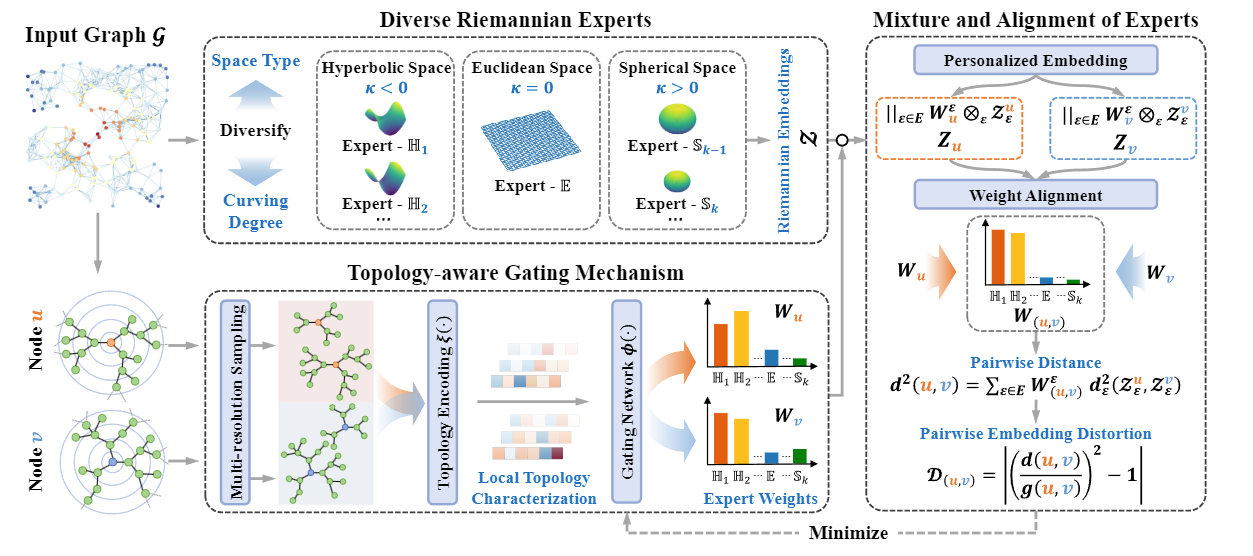
4.1 多样化黎曼专家 Diverse Riemannian Experts

图的子结构仍然很复杂，单一的常曲率空间不足以很好的匹配图的几何形状。因此，这里考虑采用多个具有不同曲率的黎曼空间来更好地建模局部拓扑。这里将为每个专家模型设计为不同曲率空间中的黎曼图神经网络。并通过门控网络提供个性化的混合曲率空间。

黎曼图神经网络。我们首先简要介绍以$\kappa$-球极投影模型（$\kappa$-stereographic model）为骨干的黎曼专家的操作。$\kappa$-球极投影模型具有一个统一的框架来描述具有正曲率，负曲率和零曲率的流形，这是一个光滑流形。$\mathcal{M}^d_\kappa=\{x\in\mathbb{R}^d|-\kappa\Vert x\Vert^2<1\}$。当$\kappa>0$时，$\mathcal{M}_\kappa^d$是球极投影球面模型；当$\kappa<0$时，$\mathcal{M}_\kappa^d$是半径为$\dfrac{1}{\sqrt{-\kappa}}$的庞加莱秋模型。

$\kappa$-球极投影模型中黎曼图神经网络的信息传递与聚合可以表述为：

$$\hat{h}_u^{(l+1)}=\text{Agg}(\log_0^\kappa(h_v^{(l)},v\in\mathcal{N}(u))),\tag{1}$$

$$h_u^{(l+1)}=\exp_0(\text{Comb}(h_u^{(l)},\hat{h}_u^{(l+1)})),\tag{2}$$

其中$\log_0^\kappa$和$\exp_0^\kappa$分别为指数映射和对数映射，$\mathcal{N}(\cdot)$表示邻接节点。$\text{Agg}(\cdot)$和$\text{Comb}(\cdot)$是邻居聚合算子和组合算子。$h_u^{(l)}$和$h_u^{(l+1)}$分别表示节点$u$在第$l$层和第$l+1$层的嵌入特征，且特征始终处于$\kappa$-球极投影模型定义的黎曼流形中。$\hat{h}_u^{(l+1)}$指节点$u$在第$l+1$层的“中间聚合特征”，是对邻居节点特征处理后得到的临时结果。

(1)式先对每个节点$u$的邻居节点$v$的第$l$层特征从$\kappa$-球极投影模型映射到参考点0的切空间（欧氏空间），再进行聚合操作。

(2)式将两个结果进行特征组合，再映射回$\kappa$-球极投影模型。

通过 “对数映射→切空间运算→指数映射” 的流程，巧妙避开了黎曼流形上直接运算的复杂性，同时保留了流形的弯曲特性。

专家多样性。为增强对复杂拓扑模式的建模能力，这里从曲率空间类型和空间弯曲程度两方面考虑黎曼专家的多样性。我们仍然按上述将黎曼专家分为三类，即双曲空间$\mathbb{H}$，球面空间$\mathbb{S}$和欧几里得空间$\mathbb{E}$，其中欧几里得空间是曲率为零的$\kappa$-球极投影模型的特例。考虑到黎曼图神经网络仅在相对有限的范围内对曲率进行微调（Fu et al.2021），曲率的初始值至关重要，这意味着即便已考虑曲率空间类型，仍需考虑空间的弯曲程度。因此，我们为每种类型的黎曼专家分配差异化的值对它们的曲率进行初始化。不同的黎曼专家表示为𝟚$E=\{E_{\mathbb{H}_1},E_{\mathbb{H_2}},\dots,E_\mathbb{E},\dots,E_{\mathbb{S}_K}\}$，每个专家对应不同曲率空间中的一个黎曼图神经网络。因此，我们可以通过将不同黎曼专家的表示与门控网络的输出进行融合，灵活地构建个性化嵌入空间，从而具备对不同拓扑模式进行建模的能力。

4.2 拓扑感知门控机制 Topology-aware Gating Mechanism

现实世界图的子结构拓扑模式（如树状、环状）往往不明确且随分辨率变化，难以直接划分并匹配嵌入空间。该门控机制的核心目标便是突破这一限制：一方面通过多分辨率采样与编码，全面提取节点局部拓扑特征；另一方面以 “最小化嵌入失真” 为导向，为每个节点动态分配适配的黎曼专家权重，最终将节点路由至最适合其拓扑模式的嵌入空间（如树状结构匹配双曲空间、环状结构匹配球面空间）。

多分辨率局部拓扑编码（Multi-resolution Local Topology Encoding）。为了提取节点周围拓扑的特征，我们首先考虑以节点为中心的局部拓扑采样：

$$s_v=\text{Sampler}(v,r)\tag{3}$$

其中$s_v$表示围绕节点v的多分辨率采样子图，$\text{Sampler}(\cdot,\cdot)$表示采样策略（可以灵活选择），$r$表示采样尺度，由于局部几何特性随分辨率的变化表现不同，我们通过式（3）进行多分辨率局部拓扑采样。

$$\mathcal{S}_v=\{\text{Sampler}(v,r),r\subset\mathcal{R}\}\tag{4}$$

其中$\mathcal{S}_v$表示节点$v$的多分辨率采样子图集，$\mathcal{R}$​式采样尺度集合。

不同分辨率的子图能反映节点局部拓扑的多维度特征（例如小尺度子图体现直接邻居关系，大尺度子图体现更远距离的结构关联），避免单一分辨率下拓扑信息的遗漏。

然后，我们引入了一个用于编码局部拓扑的GNN模型$\xi(\cdot)$,对每个采样子图$s\in\mathcal{S}_v$进行嵌入编码。再通过池化操作整合不同分辨率子图的特征，最后拼接得到节点$v$的最终局部拓扑特征$\mathcal{T}_v$。

$$\mathcal{T}_v=\Vert\text{Pooling}(\xi(s),s\in\mathcal{S}_v)\tag{5}$$

$\Vert$表示拼接操作，$\text{Pooling}(\cdot)$表示池化函数。

这里的GNN编码确保能捕捉子图的结构信息，池化与拼接则将多分辨率特征融合为统一的向量，最终得到的$\mathcal{T}_v$可精准表征节点$v$周围的几何属性。

失真引导门控网络（Distortion Guided Gating Network）。在对所有节点的局部拓扑进行编码后，我们估计节点周围的局部几何属性，为节点分配黎曼专家权重，实现嵌入空间的智能路由。

门控网络$\phi(\cdot)$接收局部拓扑特征$\mathcal{T}$，然后输出每个节点不同黎曼专家的权重。

$$\mathbf{W}_v=\text{Softmax}(\phi(\mathcal{T}_v))\tag{6}$$

其中$\mathbf{W}_v=\{\mathbf{W}_v^\varepsilon,\varepsilon\in E\}$($E$是黎曼专家集合)，每个元素$\mathbf{W}_v^\varepsilon$表示节点$v$分配给第$\varepsilon$个黎曼专家的权重，权重的和为1，故权重越高的专家，其对应的曲率空间越适合该节点的拓扑模式。

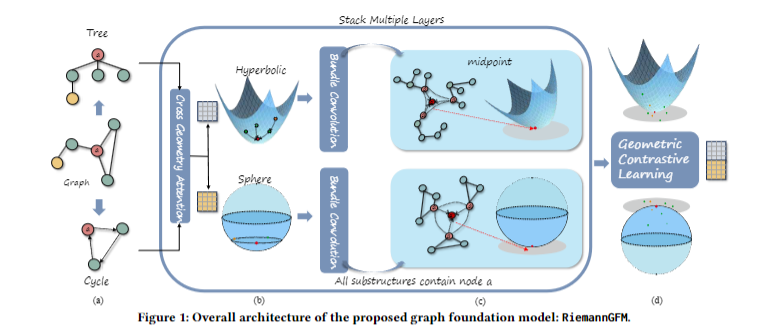
对于特定的拓扑模式，门控网络应为适当的黎曼专家提供更高的权重。对于图1中的示例，节点$u$周围的拓扑是树状的，因此门控网络的输出更偏向与具有负曲率的双曲黎曼专家。（若为环状结构，分配给正曲率的球面黎曼专家）。

为了让门控网络具备上述匹配能力，文章引入“嵌入失真损失”作为优化目标，本质是衡量 “黎曼嵌入空间距离” 与 “原图结构距离” 的一致性，通过最小化该损失推动门控网络分配合理专家权重。

$$\mathcal{L}_D=\dfrac{1}{\vert\mathcal{V}\vert^2}\sum_{i,j\in\mathcal{V}}\left|(\dfrac{d(i,j)}{g(i,j)})^2-1\right|\tag{7}$$

其中$|\mathcal{V}|$是图中的节点总数，$g(i,j)$是原图中节点$i$与$j$的最短路径距离，$d(i,j)$是嵌入空间中的距离。

通过该损失的约束，门控网络能自动学习到 “拓扑模式 - 曲率空间” 的匹配关系（例如树状拓扑的节点会被分配更高的双曲专家权重，以降低失真）。

4.3 专家的混合和对齐 Mixture and Alignment of Experts

基于门控机制输出的专家权重，将不同曲率空间的专家表示融合为节点专属的混合嵌入空间，并通过对齐策略实现跨空间距离的合理计算，确保嵌入既保留局部拓扑特性，又支持全局节点的交互分析。

黎曼专家的输出表示为$\mathcal{Z}=\{\mathcal{Z}_\varepsilon,\varepsilon\in E\}$，节点$v$的嵌入可以表示为：

$$\mathbf{Z}_v=||_{\epsilon\in E}\mathbf{W}_v^\varepsilon\otimes_\epsilon\mathcal{Z}_\varepsilon^v\tag{8}$$

• $\mathbf{Z}_\varepsilon^v$：节点$v$在第$\varepsilon$个黎曼专家中的嵌入表示
• $\mathbf{W}_v^\varepsilon$：由拓扑感知门控机制输出的节点$v$分配给第$\varepsilon$个专家的权重。
• $\otimes_\varepsilon$：（流形乘积操作）定义在第$\varepsilon$个专家对应流形上的乘积运算，具体为$w\otimes_\varepsilon x=\exp_\varepsilon^0(w\cdot\log^0_\varepsilon(x))$本质是 “按权重缩放流形上的嵌入特征”，确保融合过程符合流形几何约束
• $||_{\varepsilon\in E}$：（拼接操作）将所有专家经“权重乘积”后的嵌入结果进行拼接。

由于不同节点的混合嵌入空间存在差异（如节点$u$偏向双曲、节点$v$偏向球面），直接计算它们在各自空间中的距离会产生严重偏差（如双曲空间的距离尺度与球面不同）。专家对齐的核心是 “生成跨空间的中性/偏向性对齐权重，加权计算距离”，具体通过公式（9）和（10）实现。

我们考虑每个节点对$(u,v)$对齐的专家权重：

$$\mathbf{W}_{(u,v)}=\text{Softmax}(\mathbf{W_u}\cdot\mathbf{W_v})\tag{9}$$

例如图1中节点$u,v$都偏向双曲专家，$\mathbf{W}_{(u,v)}$会显著提高双曲专家的权重，降低其他的权重；而当二者差异较大时，则会在两者偏好间去中性。

节点之间的嵌入距离表示如下：

$$d^2(u,v)=\sum_{\varepsilon\in E}\mathbf{W}^\varepsilon_{(u,v)}d^2_\varepsilon(\mathcal{Z}^u_\varepsilon,\mathcal{Z}^v_\varepsilon)\tag{10}$$

$d^2_\varepsilon(\mathcal{Z}^u_\varepsilon,\mathcal{Z}^v_\varepsilon)$表示节点、$u、v$在第$\varepsilon$个专家对应曲率空间中的距离平方。再通过加权求和得到最终跨空间距离。

4.4 优化目标

总体优化目标由下游任务目标和嵌入失真的最小化组成。

$$\mathcal{L}=\mathcal{L}_{\text{task}}+\lambda\mathcal{L}_\mathcal{D}\tag{11}$$

• $\mathcal{L}_{\text{task}}$保障 “任务有效性”：确保模型的核心输出能满足实际应用需求（如准确预测节点类别、判断链路是否存在），是模型的 “功能导向”；
• $\mathcal{L}_\mathcal{D}$保障 “拓扑保真度”：确保节点嵌入始终与原图拓扑结构保持一致，避免嵌入失真导致的结构信息丢失，是模型的 “结构导向”；
• 超参数$λ$实现 “动态平衡”：通过调整$λ$，可根据任务优先级灵活适配 —— 例如在对拓扑结构敏感的任务（如分子结构分析，需精准保留原子连接关系）中，可增大$λ$；在对拓扑要求较低、仅需类别区分的任务（如简单节点分类）中，可减小$λ$。

4.5 能动性分析

时间复杂度为$O(|\mathcal{R}||\mathcal{D}|+|\mathcal{D}_s|+K|\mathcal{D}|)$。

• $O(|\mathcal{R}||\mathcal{D}|)$代表局部拓扑采样的复杂度：尺度数量乘以输入图的规模。
• $O(|\mathcal{D}_s|)$代表门控机制的复杂度：采样子图的总规模。
• $O(K|\mathcal{D}|)$代表多样黎曼专家的复杂度：黎曼专家的数量乘以图规模。

整体复杂度为线性复杂度，计算效率高。

算法：GraphMoRE完整训练流程

• 输入：待处理图$\mathcal{G}$、黎曼专家数量$K$，初始曲率集合$C$、训练轮次$T$。（黎曼专家的数量设置为5，初始曲率为{-3， -1， 0， 1， 3}。）
• 输出：下游任务的预测结果。

1. 初始化：通过初始曲率集合$C$初始化$K$个黎曼专家，每个专家对应一个特定曲率的$\kappa$-球极投影模型。
2. 预处理：局部拓扑子图采样，按照公式（4），$\mathcal{S}_v=\{\text{Sampler}(v,r),r\subset\mathcal{R}$ 为每个节点采样$|\mathcal{R}|$个不同尺度的局部子图，得到子图集$S$
3. 训练轮次循环（$T$轮）：每轮训练按“专家编码→门控权重计算→专家混合与对齐→参数更新” 的顺序执行
   1. 各个黎曼专家独立编码：对于每个黎曼专家$\varepsilon$基于公式（1）$\hat{h}_u^{(l+1)}=\text{Agg}(\log_0^\kappa(h_v^{(l)},v\in\mathcal{N}(u)))$和公式（2）$h_u^{(l+1)}=\exp_0(\text{Comb}(h_u^{(l)},\hat{h}_u^{(l+1)}))$对全图节点执行信息传递与聚合，输出该专家空间下的节点嵌入$\mathcal{Z}_\varepsilon$(每个节点对应一个$\mathcal{Z}_\varepsilon$向量)。
   2. 拓扑感知门控机制：先按公式（5）$\mathcal{T}_v=\Vert\text{Pooling}(\xi(s),s\in\mathcal{S}_v)$对采样得到的子图集$S$进行编码与池化，得到每个节点的局部拓扑特征$\mathcal{T}$,再按公式（6）$\mathbf{W}_v=\text{Softmax}(\phi(\mathcal{T}_v))$，输出每个节点分配给各专家的权重$\mathbf{W}$
   3. 专家混合与对齐：按照公式（9）$\mathbf{W}_{(u,v)}=\text{Softmax}(\mathbf{W_u}\cdot\mathbf{W_v})$对每对节点$(u,v)$计算对齐专家权重$\mathbf{W}_{(u,v)}$，解决跨空间权重偏差；再按照公式（10）$d^2(u,v)=\sum_{\varepsilon\in E}\mathbf{W}^\varepsilon_{(u,v)}d^2_\varepsilon(\mathcal{Z}^u_\varepsilon,\mathcal{Z}^v_\varepsilon)$计算节点对在对齐空间中的嵌入距离，为下游任务（如链路预测的相似度判断）提供依据。
   4. 参数更新：按照公式（11）$\mathcal{L}=\mathcal{L}_{\text{task}}+\lambda\mathcal{L}_\mathcal{D}$最小化参数$\mathcal{L}$

5 实验验证

5.1 实验配置

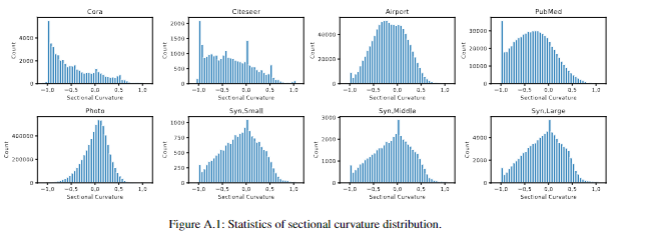
数据集。使用引文网络Cora（Sen et al. 2008）、Citeseer（Kipf and Welling 2017）、PubMed（Namata et al. 2012），航空网络Airport（Chami et al. 2019），共购网络Photo（Shchur et al. 2018）等五个真实数据集，并额外合成了包含多种拓扑结构的拓扑异质性合成图（小中大三种图）进行进一步比较。

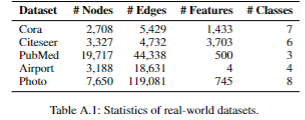
文章通过分析图的截面曲率来探索拓扑异质性。给定一个节点集为$\mathcal{V}$的图$\mathcal{G}$，可以计算由节点$m$及其相邻节点$b,c$组成的测地三角形的截面曲率：

$g(a,b)$是图上节点a和b之间的最短路径距离。

基线：选择3种欧氏空间GNN：GCN、GAT、SAGE；7种黎曼空间GNN：HNN、HGCN、$\kappa$-GCN、LGCN、Q-GCN、MotifRGC、GraphMoRE。

设置：将所有方法的层数设置为2，对于其他模型设置采用相应论文的默认值，并在十次独立运行中取平均值。

5.2 结果评估

真实图数据集的性能：评估了再链路预测和节点分类任务的方法，精度最高且稳定性最强。

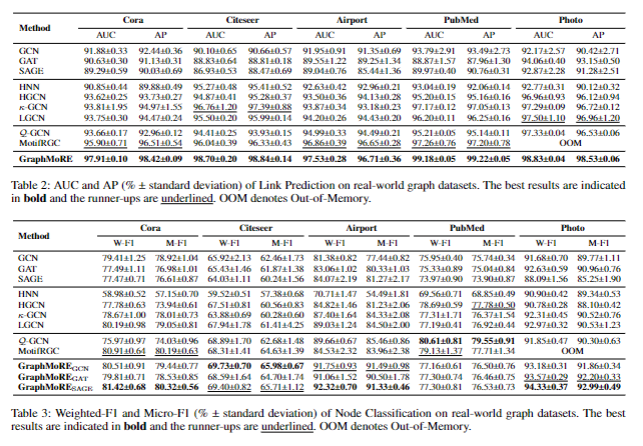
AUC（Area Under the ROC Curve，ROC 曲线下面积）

1. 核心定义：
   AUC 是 “受试者工作特征曲线（ROC 曲线）” 与横轴之间的面积，取值范围为 [0,1]。ROC 曲线以 “假正例率（FPR，错误预测存在边的比例）” 为横轴，以 “真正例率（TPR，正确预测存在边的比例）” 为纵轴，描述模型在不同阈值下的分类性能。

合成图中的性能：

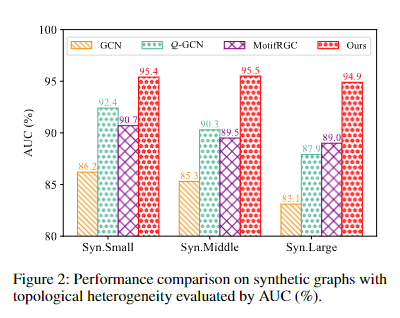
GraphMoRE在面对大规模图性能几乎无衰减，且保持高精准度。

消融研究：我们在两个下游任务上使用四种变体进行消融研究，以验证 GraphMoRE 中每个组件的有效性。在这里使用 GCN 作为节点分类任务的分类器主干。事实证明缺少任何组件都会导致性能下降。

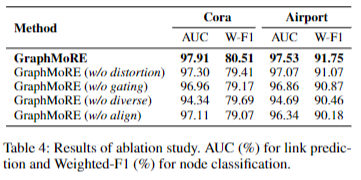
嵌入失真分析：为验证 “个性化混合曲率空间” 对拓扑结构的保留能力，实验通过表 5 量化各方法的嵌入失真（$\mathcal{L}_D$，数值越低，嵌入空间与原图拓扑一致性越强），核心结论如下：

GraphMoRE 在所有数据集上的嵌入失真均最低，例如 Cora 数据集失真仅 0.22，远低于 Q-GCN（0.80）、MotifRGC（0.69）；PubMed 数据集失真 0.18，低于 κ-GCN（0.45）。这证明其通过 “失真引导门控网络” 与 “专家混合”，能最小化嵌入空间与原图的拓扑偏差，为下游任务提供高质量的节点表示。

图中越红扭曲越多。

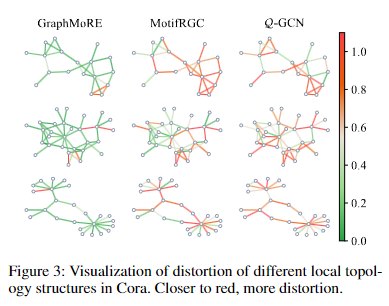
6 总结

本文提出了一种新的方法 GraphMoRE，从局部拓扑表征的角度解决拓扑异质性问题。我们首先提出了一种拓扑感知门控机制，该机制通过估计局部几何属性来单独选择节点的最佳嵌入空间。然后，我们设计了多样化的黎曼专家，灵活地构建个性化的混合曲率空间，有效地将图嵌入到不同点具有不同曲率的异质流形中。最后，我们提出了一种简洁有效的对齐策略来公平地测量不同嵌入空间之间的成对距离。广泛的实验表明了 GraphMoRE 在拓扑异质性方面的优势。未来的工作将进一步探索黎曼 MoE 在增强图基础模型统一处理来自各种类型和领域的不同图数据的能力方面的潜力和更广泛的影响。