论文解读：A Unification Framework for Euclidean and Hyperbolic Graph Neural Networks

本文最后更新于16 天前，其中的信息可能已经过时，如有错误请发送邮件到lieyin2333@163.com <br> 如遇到公式没有加载成功，请刷新几次或耐心等待

A Unification Framework for Euclidean and Hyperbolic Graph Neural Networks

发布于 IJCAI-23 https://arxiv.org/abs/2206.04285

如果遇到公式无法正常加载等情况，请耐心等待或多次刷新即可。

Introduction

尽管双曲神经网络在层级图数据处理中表现出色，但当前模型仍存在三大关键问题：

双曲模型运行在全新的流形上，依赖独特的旋量向量空间（gyrovector space），与欧几里得向量空间差异显著，导致单一层内会纠缠多个不一致的向量空间，增加模型复杂性。
由于流形特性不同，欧几里得空间中常用的 Dropout、L1/L2 正则化等技术在双曲模型中无法保证效果；同时，将复杂欧几里得架构（如多头注意力网络）迁移到双曲空间时，受黎曼流形特殊性质影响，转换过程非直观且难度大。
双曲算子需执行大量复杂数学运算（如莫比乌斯变换），与欧几里得图神经网络相比，其原始算子的计算量更大。

为解决上述问题，本文提出以庞加莱圆盘模型（Poincaré Disk Model）作为搜索空间，将所有近似运算均在圆盘上执行，且将圆盘视为从原点衍生的切空间，从而彻底摒弃传统双曲模型中频繁的 “空间间变换”（如双曲流形与欧几里得切空间的反复切换）。

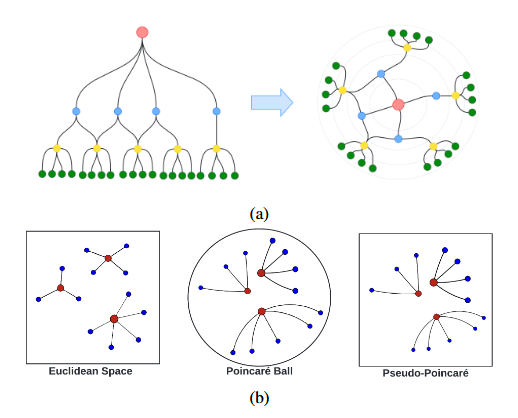
文章提出双曲归一化层（hyperbolic normalization layer）；其次将整个双曲模型简化为 “欧几里得模型 + 双曲归一化层” 的级联结构——通过用欧几里得运算替代不可扩展的旋量向量/莫比乌斯运算，同时保留黎曼流形特性（借助双曲归一化层与黎曼优化器），最终形成伪庞加莱框架（如图 1.b 所示）。

双曲神经网络

双曲神经网络的设计源于流形假设：高维数据通常分布在低维流形的邻域内，模型通过学习这一低维流形，能更精准地捕捉数据点间的关联关系。对于图数据而言，层级结构（如树状图、知识图谱中的实体层级）极为常见，而这类结构与双曲流形的特性高度适配：双曲空间的体积随半径呈指数增长，可与层级结构中 “节点数量随深度指数增加” 的规律相匹配，从而以低失真度嵌入层级图数据。

双曲空间的数学性质：双曲空间是具有常负曲率的黎曼流形，其坐标可通过多种等距模型表示，本文选择庞加莱球模型（Poincaré Ball Model），记为$\mathbb{B^n_c}$，作为研究对象。该模型是当前双曲网络中应用最广泛的形式，且易于与神经网络组件结合。在庞加莱球模型中，曲率$c$是核心参数，不同曲率会影响空间的 “扩张程度”，进而影响层级结构的嵌入效果。

基本运算：莫比乌斯运算 向量加法：$\oplus_c$ 标量乘法：$\otimes_c$

空间转换：对数、指数映射 指数映射（切空间到双曲空间）：

$$ p=\exp^c_v(x)=v\oplus_c(\tanh(\frac{\lambda_v||x||}{2})\frac{x}{||x||})\tag{1} $$

对数映射（双曲空间到切空间）：

$$ x=\log^c_v(p)=\frac{2}{\lambda_v}\tanh^{-1}(||-p\oplus_cv||)\frac{-p\oplus_cv}{||-p\oplus_cv||}\tag{2} $$

双曲空间的切空间近似依赖空间局部性假设：即切空间中的向量需足够小，且靠近基点v，才能确保映射到双曲空间后的误差较小。此外，当需要将一个切空间的向量传输到另一个基点的切空间时（如双曲线性层中的偏置加法），需采用平行传输（Parallel Transport） 技术，该技术可在保持向量方向与长度特性的前提下，实现跨基点的向量传递。

双曲层的实现

双曲前馈层

对于欧氏空间中的函数$f:\mathbb{R}^n\to\mathbb{R}^m$，它的莫比乌斯版本为：$f^{\otimes_c}(p):=\exp^c_0(f(\log^c_0(p)))$。欧几里得线性层$h^\mathbb{R}(x)=Wx$，$W\in\mathbb{R}^{n\times m}$为权重矩阵，的双曲等价形式为：

$$ h^\mathbb{B}(p)=\frac{\tanh(\frac{|Wp|}{|p|}\tanh^{-1}(\sqrt{c}|p|))}{\sqrt{c}|Wp|}Wp\tag{3} $$

双曲卷积层

线性变换：对每个节点$p_i$的双曲表示进行莫比乌斯线性变换与偏置添加

$$ h^\mathbb{B}(p_i)=W_i\otimes_cp_i\oplus_cb_i $$
邻域聚合：将变换后的邻域特征映射到中心节点p0的切空间中，通过加权求和实现聚合

$$ h^\mathbb{B}_{agg}(p_0)=\exp^c_{p_0}(\sum^k_{i=0}w_{ij}\log^c_{p_0}(h^\mathbb{B}(p_i))) $$

$w_{ij}=\text{softmax}^k_{i=1}(MLP(\log^c_0(p_0)||\log^c_0(p_i)))$表示邻居节点的聚合权重
激活与映射：将聚合结果映射到原点的切空间，经过激活函数（如 sigmoid）后，再映射回双曲空间，得到最终卷积输出

$$ GCN^{\oplus_c}(p_0)=\exp^c_0(\sigma(\log^c_0(h^\mathbb{B}_{agg}(p_0))))\tag{4} $$

多关系双曲表示层

该层通过评分函数建模实体与关系的关联，核心是将欧几里得空间的距离度量替换为双曲距离。

对于知识图谱中的三元组$(h,r,t)$（$h$为头实体，$r$为关系，$t$为尾实体），欧几里得评分函数通常为$\phi(x_h,x_r,x_t)=-||Rx_h-(x_t\pm x_r)||^2$（$R$为关系对角矩阵），双曲评分函数基于双曲距离构建：

$$ d^\mathbb{B}(p_1,p_2)=\frac{2}{\sqrt{c}}\tanh^{-1}(\sqrt{c}||-p_1\oplus_cp_2||)\tag{5} $$

伪庞加莱双曲网络Pseudo-Poincaré Hyperbolic Networks

尽管双曲网络在层级图嵌入中具有较大优势，但仍存在上述提到的三个缺陷：计算成本高、可拓展性弱、正则化与随机性操作不可靠。此外，传统双曲网络还隐含一个关键假设：嵌入向量在所有维度均满足空间局部性（spatial locality），即嵌入点需靠近切空间基点 v，才能保证切空间近似的准确性。但实际场景中，图数据的嵌入向量常因层级跨度大、节点关联性复杂，难以在所有维度满足空间局部性，导致切空间近似误差显著，反而降低模型性能。

为解决上述问题，本文提出将所有切空间近似固定于原点，而非动态变化。由此我们可以大幅减少参数数量与运算步骤，同时可以拜托空间局部性假设的束缚。此外只有在原点处的切空间与庞加莱半平面模型存在一一映射关系，这种对应性允许将切空间近似与半平面模型结合，所有近似运算可在半平面内统一执行，既保留双曲空间的层级表达能力，又降低空间变换的复杂度，使模型更易理解、开发与优化。

固定为原点后，指数映射与对数映射可被大幅简化：

$v=0$时，$\oplus_c$在原点处满足$0\oplus_ca=a$，同时庞加莱球模型中原点处的共性因子$\lambda_v\equiv \dfrac{2}{\sqrt{c}}$。

代入后公式（1）、（2）简化为：

$$ p=\exp^c_0(x)=\frac{\tanh(\sqrt{c}|x|)}{\sqrt{c}|x|}x\tag{6} $$

$$ x=\log^c_0(p)=\frac{\tanh^{-1}(\sqrt{c}|p|)}{\sqrt{c}|p|}p\tag{7} $$

我们可以通过公式（6）、（7）重构双曲前馈层，卷积层、注意力层和多关系层的重构方法类似。

伪庞加莱前馈层

Lemma 1 对于原点处切空间的点$x\in \mathcal{T}_{0_n}\mathbb{B}^n_c$，将其映射到双曲空间$\mathbb{B}^n_c$的指数映射$\exp^c_0:\mathcal{T}_{0_n}\mathbb{B}^n_c\to\mathbb{B}^n_c$，$\exp^c_0(x)$等价于用一个非线性标量函数$\omega:\mathbb{R}^n\to\mathbb{R}^n$对输入向量$x$进行缩放，即：

$$ p=\exp^c_0(x)=\omega(x)x;\;\;\;\omega(x)=\frac{\tanh(\sqrt{c}|x|)}{\sqrt{c}|x|}\tag{8} $$

其中$\omega(x)$是用于指数映射的双曲归一化因子，该结论可由公式（1）推导。

Lemma 2 设$f^{\otimes_c}$为单个双曲前馈层，$f$为对应的欧几里得前馈层。若在所有运算阶段均基于原点处的切空间进行近似，则$n$个双曲前馈层的级联$F^{\otimes_c}=\{f^{\otimes_c}\}^n_{i=1}$等价于将$n$个对应的欧几里得前馈层的级联$F_n=\{f_i\}^n_{i=1}$包裹在对数映射$\log^c_0$与指数映射$\exp^c_0$之间，即：

$$ F_n(x)=f_n(f_{n-1}(\cdots f_1(x))) $$

$$ F^{\otimes_c}_n(p)=f^{\otimes_c}_n(f^{\otimes_c}_{n-1}(\cdots f^{\otimes_c}_1(p)))=\exp^c_0(F_n(\log^c_0(p)))\tag{9} $$

proposition 引理2表明，若要在欧几里得网络中捕捉层级结构，仅需在初始阶段和最终阶段运用双曲变换指数映射和对数映射即可。

Lemma 3 对于给定的输入特征$x=\log^c_0(p)\in\mathbb{R}^n$，给定的双曲前馈层可重写为如下形式：$f^{\otimes_c}(x):=\omega(f(x))\cdot f(x)$

由引理2和3，我们可以得出关于级联双曲层的下述定理

Theorem 4 将切空间始终固定于原点时，针对欧几里得输入$x\in\mathbb{R}^n$的级联双曲前馈层$F^{\otimes_c}$可重写为如下形式：$F^{\otimes_c}_n(x):=\Omega(F_n(x))\cdot F_n(x)$，其中$\Omega(F_n(x))$是级联双曲前馈网络的双曲归一化因子。需要注意的是，$\omega()$是变量层面的指数变换因子，而$\Omega()$是神经网络层面的同类因子。

传统网络中，每一层的输入需先通过对数映射投影到欧几里得空间执行计算，再通过指数映射投影回双曲空间，存在频繁的空间切换，计算成本高。而通过双曲归一化的引入，级联双曲层可在欧几里得空间中完成所有前馈计算（$F_n(x)$），仅在最终阶段通过$\Omega(F_n(x))$执行一次双曲归一化，即可将结果映射到双曲空间。

算法：

输入：欧几里得模型$F_L$、样本节点$x\in\mathbb{R}^n$ 输出：归一化双曲模型$F^{\otimes_c}_L(x)$ $f^{\otimes_c}_0(x)=x$ 对于层数$l$：$1\to L$执行： $x\leftarrow f^{\otimes_c}_{l-1}(x)$ 欧几里得模型的第$l$层为$f_l(x)$ $\omega(f_l(x))=\frac{\tanh(\sqrt{c}||f_l(x)||)}{\sqrt{c}||f_l(x)||}$；公式（8） $f_l^{\otimes_c}(x)=\omega(f_l(x))\cdot f_l(x)$；引理3 返回$F_n^{\otimes_c}(x)=f^{\otimes_c}_L(x)$

伪庞加莱层

伪庞加莱卷积层

伪庞加莱图卷积将聚合权重和聚合函数在原点切空间$\mathcal{T}_0\mathbb{B}^n_c$，对于具有邻居节点$\{p_i\}^k_{i=1}$的根节点$p_0$，其聚合结果为：

$$ h^\mathbb{B}_{agg}(p_i)=\exp^c_0(\sum^k_{i=0}w_{ij}\log^c_0(h^\mathbb{B}(p_i)))\tag{10} $$

结合论文定理4，伪庞加莱图卷积将传统双曲图卷积层$GCN^{\otimes_c}:\mathbb{B}^n_c\to\mathbb{B}^m_c$重构为归一化GCN，$NGCN^{\otimes_c}:\mathbb{R}^n\to\mathbb{R}^m$，将欧氏空间特征输出为欧氏空间中的双曲归一化特征：$NGCN^{\otimes_c}(x_0)=\Omega(GCN(x_0))\cdot GCN(x_0)$。

论文指出，尽管伪庞加莱图卷积的嵌入存在少量噪声，但由于层级结构本身具有 “松散的空间局部性”（如树结构中父节点与子节点的特征差异较小），这种噪声对性能影响极小；反而因计算效率提升和欧氏正则化的可复用性（如 dropout、L2 正则）

伪庞加莱图注意力层

$NGAT^{\otimes_c}(x)=\Omega(GAT(x))\cdot GAT(x)$

伪庞加莱多关系表示

传统双曲多关系模型计算实体间距离时，依赖复杂的莫比乌斯运算和双曲距离公式（公式5），同样计算成本高且易受空间局部性假设限制。

伪庞加莱统一在原点切空间近似，则将距离重构为：$d^\mathbb{B}(x_1,x_2)=\omega(x)d^\mathbb{R}(x_1,x_2)$

在知识图谱等多关系场景中，模型需通过 “评分函数” 衡量三元组 $(h,r,t)$（头实体-关系-尾实体）的合理性。伪庞加莱框架将传统双曲评分函数$\phi^\mathbb{B}(p_h,p_r,p_t)$近似为 “欧氏评分函数+双曲归一化” 的形式，即 NMuR（Normalized Multi-relational Representation）

首先定义基于欧氏距离的基准评分函数：

$$ \phi^\mathbb{R}(x_h,x_r,x_t)=-d^\mathbb{R}(Rx_h,x_t+x_r)^2\tag{11} $$

其次进行双曲归一化得到伪庞加莱评分函数：

$$ NMuR^\mathbb{B}(x_h,x_r,x_t)=\Omega(\phi^\mathbb{R}(x_h,x_r,x_t))\phi^\mathbb{R}(x_h,x_r,x_t)\tag{12} $$

实验

问题 1：在节点分类与链路预测任务中，伪庞加莱变体模型与对应的欧氏模型、双曲模型相比，性能表现如何？
问题 2：在知识图谱推理任务中，伪庞加莱变体模型与对应的欧氏模型、双曲模型相比，性能表现如何？
问题 3：优化器的选择对伪庞加莱变体模型有何影响？这一选择会对模型的运行时间产生怎样的作用？此外，双曲归一化与其他归一化方式相比，效果有何差异？
问题 4：将伪庞加莱变体模型应用于深度图神经网络（GNN）架构（如 GCNII）时，其性能表现如何？
问题 5：通过双曲投影与伪庞加莱投影得到的表示向量，二者存在哪些差异？

数据集：Cora、Citeseer、Pubmed、Amazon-Photo、WN18RR、FB15k-237、PPI

基线：GCN、GAT、HGCN、HGAT、MuRE、MuRP、RGCN、GCNII

问题1 图预测任务性能

几乎在所有情况下伪庞加莱变体模型优于欧式模型，且仅在链路预测任务中，性能略低于双曲模型。这是因为在同质图的链路预测任务中，相邻节点的向量往往具有空间局部性，节点分类中则局部性较弱（例如，距离较远的节点仍可能属于同一类别）。

值得注意的是，无论数据集的双曲性如何，伪庞加莱变体模型在所有节点分类数据集上的性能均优于欧氏模型，这表明他具有比纯双曲模型更强的通用性。

问题2 多关系推理任务性能

MRR（Mean Reciprocal Rank）：所有正确实体在预测排序中的 “倒数排名” 的平均值，值越高表示正确实体的排序越靠前，推理精度越高；
Hits@k（k=1, 3, 10）：正确实体进入预测结果前k名的比例，值越高表示模型的推理召回能力越强。

NMuR在低纬度全面超越欧氏和双曲模型，在高纬度下与双曲模型MuRP基本持平但计算效率大幅提升。

将伪庞加莱框架应用于RGCN的方法与实验

论文直接复用[Thanapalasingam et al., 2021] 已实现的PyTorch版本 RGCN 模型，仅在模型的最后一层添加伪庞加莱框架的双曲归一化层，并使用Riemann Adam优化器训练。

问题3：模型分析

优化器选择

执行时间对比

归一化方式对比

问题4：双曲归一化在深度GNN中的应用

在不同层数的模型中，经过归一化改造的 N-GCNII 模型（伪庞加莱变体 GCNII）的最优性能，要么与欧氏空间 GCNII 的最优性能持平，要么超过后者。随着网络层数的增加，两者之间的性能差距也随之缩小。我们认为，这一现象的原因在于：更深层的模型更擅长学习平滑流形（smooth manifolds——这与自然语言处理（NLP）领域的相关研究结论一致，该研究指出深度模型的潜空间具有一定程度的双曲性。

问题5：嵌入可视化

总结

在本文中，论文证明：只需通过以下两步操作，即可将一个欧氏模型改造为具备双曲模型功能的模型：（1）为其接入双曲归一化层；（2）使用黎曼优化器。

从训练角度来看，该方法使得可训练参数能在欧氏向量空间中交互，进而让模型训练过程能够利用欧氏正则化技术。此外，与现有双曲方法相比，论文所提方法的训练速度显著更快。这一特性使得双曲网络在实际应用中更具灵活性，能够适配更多样化的图问题。

从任务角度来看，论文移除了 “相邻节点需具备（全维度的）空间局部性” 这一隐含假设 —— 而该假设此前一直是双曲模型训练的必要前提。这一改进让论文提出的框架能够应用于更广泛的任务场景。